Welcome to the Quantum World: Where Certainty Ends and Possibility Begins
1. The Classical vs. Quantum World
In our everyday experience of the world, things have precise positions, speeds, and outcomes. You throw a baseball—you know where it’s going. But when we zoom in to the world of atoms and particles, things get weird — and the rules change.
2. The Probabilistic Nature (Uncertainty and Superposition)
🗨️ Metaphor:
"Imagine flipping a coin, while it is spinning in mid-air, it spins in mid-air being both at heads and tails at the same time, with the probability of being heads or tails is still 50-50. At this point, if we want to describe the state of this system (the coin), it would be a combination of both heads and tails — until you look, and then you can say whether the coin landed on heads or tails. That’s how particles behave in the quantum world: they exist in a state made of both heads and tails, a superposition of states, until they’re measured.
🎯 Main idea:
Quantum Particles don’t have exact positions or velocities—just probabilities.
Measurement collapses the particle’s wavefunction to a definite value.
Let’s look more closely at the idea that Particles behave probabilistically
In classical mechanics, we think of a particle as a tiny object with a definite position and velocity at any time. But in quantum mechanics, particles like electrons that are described by a wavefunction, a mathematical function that tells you the probability of finding the particle in different places. You can think of the particle not as a dot but as a fuzzy cloud, where he denser the cloud in one spot, the more likely the particle is to be found there.
This is why we say: "Particles don't have exact positions or velocities—just probabilities."
🎵 The Wave Nature of Matter
In our everyday life, we see systems that exhibit wave properties. Things like sound waves, water waves (surface waves), waves on a cable (vibrating), or if you live in certain places, you may experience seismic waves. These are all classical physics examples that are described by wave equations, where the disturbance propagates through a medium or field, transferring energy without necessarily transferring matter.
For example, when waves meet (i.e., waves in water), they combine through a process called interference. This can take a few forms:
· Constructive Interference: When the crests (high points) and troughs (low points) of two waves line up, they reinforce each other, creating a larger wave. Think of two ripples on a pond colliding and forming a bigger splash.
· Destructive Interference: When a crest meets a trough, they cancel out to some extent—sometimes completely—resulting in a smaller or flat wave.
This blending of energy is happening constantly in light, sound, water waves, and even quantum systems.
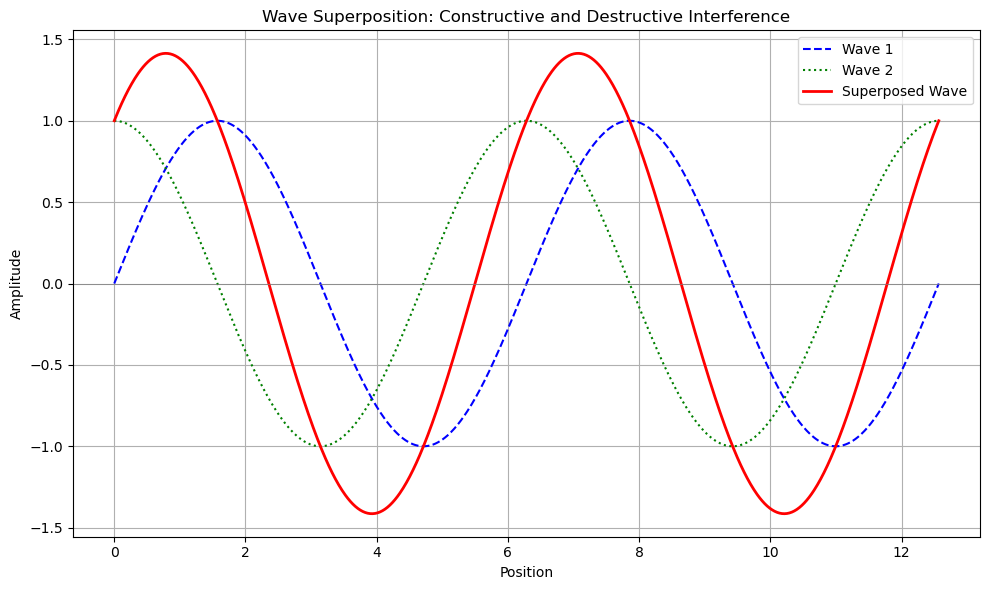
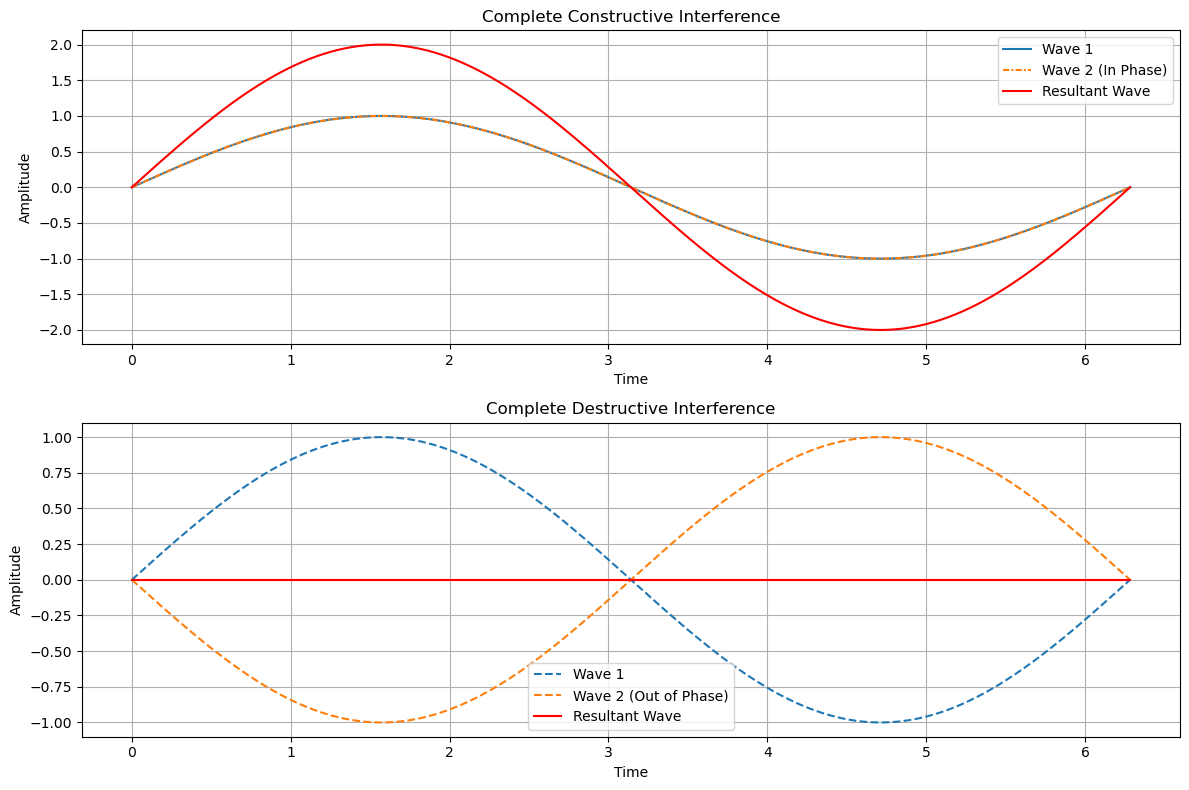
Below in Figure 1, is an example of superpositions of waves. The top image highlights full constructive interference and the bottom image shows destructive interference. You can see that the maximum of the two waves is 1 and its minimum is -1, where 1 and -1 are called the wave's amplitude. For these two points, for complete constructive interference, the superposition of these waves yields 2 (superposition means at each position point you add the two waves together) for the maximum and -2 for the minimum. For complete destructive interference, you can see the waves when at each point you add them together (superposition), completely cancel out (equal 0). This situation is often called completely out-of-phase . Using the same two points as in our constructive interference example, you now see that wave 1 equals 1 and wave 2 equals -1. In fact, for all the points, the two waves are equal but of opposite sign (meaning one is positive, say +1, and the other is -1). The superposition of these two waves produces 0 for all points.
Below in Figure 2, the waves are slightly shifted along the position axis (x-axis). Using our same points as before, you can see that the superposition wave doesn’t quite equal 2 and -2; they are less than 2 and greater than -2 (-2 is less than -1.9, say, meaning -2 does not get more negative, it is heading upwards towards 0). This is because each wave’s maximum and minimum values occur at different points in space, and this is true for the values of the superposition wave at all points in space. Imagine you fix wave 2, and you slowly pull wave 1 to the right (wave 1 could be referred to as phase-shifted relative to wave 2). The superposition wave continues to have positive values and negative values going towards 0. Once the maximums of wave 1 line up with the minimums of wave 2, the superposition wave is 0 for all points. This is the complete destructive interference as we saw in Figure 1. Now, if you continue to pull wave 1 to the right, the superposition wave starts growing, and if you keep pulling to the right, it will reach the complete constructive interference pattern like in Figure 1.
Notice the superposition wave (like the other waves) starts to repeat the pattern. The point where the pattern repeats itself would define the superposition wave’s wavelength 𝛌. Now imagine, if you had lots of waves where some are shifted relative to our wave 1, at some points in position, we will get a maximum amplitude resulting from constructive interference but necessarily complete constructive interference, giving the highest point of a wave (crest of water wave), while for others, we may get destructive interference, leading to the minimum amplitude (trough of a wave) and other intermediate amplitude that help to make-up the entire wave. Hopefully, this simplistic model helps us to understand how waves form and how you can get a big wave from many small waves.
Another feature of waves is that they have a wavelength that describes how far they propagate in space before repeating the same pattern over and over. If you remember what the mathematical functions, sine and cosine, they are waves that repeat in space and have a wavelength. Now the important part is that the momentum, p, of these waves is inversely proportional to their wavelength, that is, p=1/𝛌. So if you have a short wavelength, you have a large momentum, and vice versa.
These waves follow classical equations — disturbances that move through a medium, transferring energy. But in quantum mechanics, the wave isn't a ripple in water or air — it’s a probability wave.
Now comes the key idea: wave-particle duality. Particles act like waves. And waves behave very differently from particles in one crucial way:
A wave that's localized in space (i.e., sharply peaked in position) must be made by combining many different wavelengths. Think of a big wave in the ocean; it is formed by lots of waves coming together to form this big wave. This combining of waves also means you have a wide range of momenta.
Correspondingly, a wave with a defined momentum (i.e., well-defined momentum) must be spread out in space.
For example, let’s look at music and a pure note on a tuning fork (single frequency = defined momentum) lasts long but is hard to pin down in time (spread out). However, a short drumbeat is localized in time (defined position) but contains a spread of frequencies (momentum uncertainty).
For example, let’s look at music and a pure note on a tuning fork (single frequency = defined momentum) lasts long but is hard to pin down in time (spread out). However, a short drumbeat is localized in time (defined position) but contains a spread of frequencies (momentum uncertainty).
This is a fundamental mathematical property of waves called the Fourier transform. A Fourier transform contains both sine and cosine, just as waves, but is a more complicated function that involves complex numbers. The point about the Fourier transform is that you can obtain sine and cosine from it.
3. The Heisenberg Uncertainty Principle: Knowing Less to Understand More
One of the most famous — and misunderstood — ideas in quantum mechanics is the Heisenberg Uncertainty Principle.
It’s often summed up like this: You can’t know both where something is and how fast it’s moving — at the same time — with perfect precision.
At first glance, that sounds like a problem with our measuring tools, as if we just need better microscopes or sensors. But that’s not it.
This principle isn’t about technological limitations — it’s a fundamental property of nature.
What does it mean?
In classical physics, if you know where a car is and how fast it’s going, you can predict exactly where it’ll be a few seconds later. But in the quantum world, if you try to pin down the position of a particle more precisely, you automatically become less certain about its momentum (its speed and direction) — and vice versa.
It’s not because the particle is misbehaving — it’s because particles aren’t like tiny billiard balls. They behave like waves, and waves don’t have sharp edges.
🌀 Wave Metaphor
Think of a musical note. If a sound wave is spread out in time — like a long, steady tone — it has a very precise frequency (pitch). But if it’s a short, sharp “ping,” its frequency becomes less certain. You trade time for pitch.
In the same way, if a particle’s wave is sharply localized in space (you know where it is), the range of its momentum values must broaden. If the wave is spread out (you don’t know exactly where it is), the momentum is better defined.
🔬 So what’s uncertain?
It’s not that the particle is jittering around randomly. Instead:
Before measurement, a particle’s position and momentum are both described by a range of probabilities.
The more tightly you narrow one, the more uncertain the other becomes.
The Heisenberg Uncertainty Principle can be written down as,
𝚫p𝚫x ≤ ℏ/2
𝚫x is the uncertainty in position
𝚫p is the uncertainty in momentum
ℏ is Planck’s constant (a very small number)
Let’s try to understand this formula a little better. In quantum mechanics, particles like electrons aren’t just little dots — they also act like waves. This means we describe them with wave packets, which are like short-lived ripples or pulses spread out over space.
To make a wave packet that’s narrow in space (so we know roughly where the particle is), we have to combine many different waves (i.e., sine waves) with various wavelengths and frequencies (think back to our above example of waves).
That’s because a single sine wave, for example, stretches out infinitely — it doesn’t give you a clear position. Only by mixing waves with different wavelengths (and therefore different momenta) can we build a localized bump.
So: Precise position → requires many different wavelengths → high momentum uncertainty.
Now reverse it. If we only use one sine wave, it has a very clear wavelength (momentum), but it stretches out forever — the particle could be anywhere.
So: Precise momentum → means the particle is spread out → high position uncertainty.
This trade-off is at the heart of the uncertainty principle:
𝚫p𝚫x ≤ ℏ/2
Here, 𝚫x is the uncertainty in position, 𝚫p is the uncertainty in momentum, and ℏ is a very tiny constant from quantum physics.
The key message: > The more precisely you know where something is, the less precisely you can know how fast it's going — and vice versa.
Imagine building a short splash on a pond with water waves (see Figure-3):
A small, sharp splash uses many different ripple sizes (frequencies).
A pure, smooth ripple has just one frequency but spreads out.
That’s the uncertainty principle in action, hiding in the rhythm of waves.
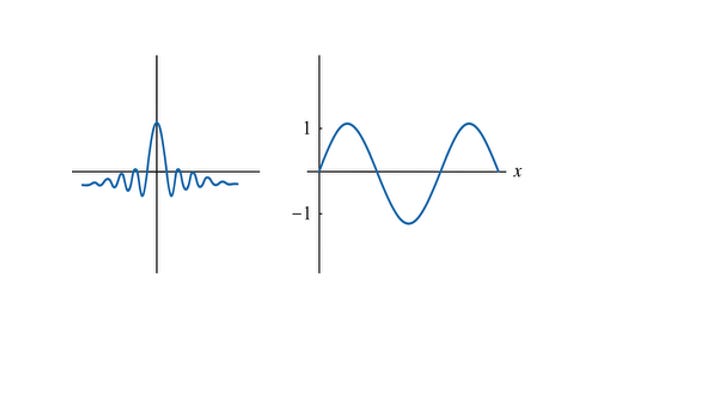
So what that tells us is that as we become more and more certain about the location of a particle (𝚫x is getting smaller and smaller, heading to 0), 𝚫p is getting larger and larger, heading to ∞. This tells us that if we knew x exactly, then we would not know the momentum p of the particle, since the uncertainty 𝚫p is infinite.
The Core Idea:
You can’t precisely know both where something is (position) and how fast it’s going or in what direction (momentum) at the same time. The more accurately you try to measure one, the fuzzier the other becomes.
🧠 Everyday Analogy:
Imagine you're trying to photograph a speeding car at night.
If you use a fast shutter, you can see exactly where the car is, but the picture will be blurry — you can’t tell how fast it was going.
If you use a slow shutter, you get a motion blur — which tells you how fast it was moving, but now you don’t know exactly where it was.
That’s the uncertainty principle in action: precision in one area means fuzziness in the other.
Again, this isn’t just a limitation of our instruments — it's a fundamental property of nature. It's like the universe itself has this built-in fuzziness at tiny scales.
This principle also tells us why electrons just don't spiral into the nucleus of an atom.
Because you can’t precisely know both the position and momentum of a particle at the same time.
If an electron got too close to the nucleus, its position would be very well known (i.e., tightly confined in space). According to the uncertainty principle, this would mean its momentum becomes highly uncertain. Because the kinetic energy is directly calculated from the momentum, and since you have large momentum fluctuations, you will have large kinetic energy.
This tells us that confining the electron too tightly costs energy — a lot of energy. That energy cost balances out the attractive pull of the nucleus. The result? The electron occupies a fuzzy “cloud” of most likely locations (remember it is based on probabilities)— what we call an orbital — and it doesn't just fall in.
This quantum balancing act gives rise to stable atoms, the periodic table, chemistry, etc.
Wave-particle duality
Wave-particle duality is one of the most astonishing ideas in modern physics. It says that tiny things—like electrons and light—can behave like particles and waves, depending on how you look at them.
Waves (like ocean waves, or ripples in a pond, or even sound waves) are spread out, continuous disturbances. They travel, they can interfere with each other (creating bigger or smaller waves), and they bend around corners. You can't point to "one wave" and say it's at a single, precise location.
Particles (like a baseball, or a tiny pebble) are distinct, localized objects. They have a definite position, mass, and can be tracked as they move from one point to another.
The Classical Difference: In our ordinary experience, something is clearly either a wave or a particle. Never both.
🌍 In the Classical World
In everyday experience:
Objects are either particles (like baseballs) or waves (like sound or water ripples).
Particles have defined positions and travel along clear paths.
Waves are spread out, overlap, and interfere, but they don't "exist" in a single spot.
Think of throwing a rock into a pond—either you're dealing with the rock or the ripples it creates, never both at once.
⚛️ In the Quantum World
The Quantum Twist: Wave-Particle Duality
But when we zoom down to the incredibly tiny, fundamental level of reality – the quantum realm – things get weird. Particles like electrons, and even light itself (which we classically considered a wave), don't always fit neatly into one category. This is wave-particle duality:
Light, for instance, can behave like a spread-out wave (which is why it can create interference patterns, just like water waves). But it can also act like a stream of tiny, discrete particles called photons (which is how it knocks electrons off a metal surface in the photoelectric effect, acting like tiny billiard balls).
Similarly, electrons (which we think of as particles making up atoms) can, under certain experimental conditions, exhibit wave-like behavior, creating interference patterns as if they were spread out and passing through multiple places at once. Yet, when we try to pinpoint their location, they act like a localized particle.
This means a single electron, shot toward a double slit, doesn't just go through one slit—it behaves as if it explores all possibilities at once, producing an interference pattern typical of waves.
🤔 So What Does This Mean?
The amazing part is that a quantum entity isn't just sometimes a wave and sometimes a particle. Instead, it possesses both wave-like and particle-like properties simultaneously, and the act of observation or the type of experiment we perform determines which aspects we will observe. You can't observe both characteristics at the same exact time in the same experiment.
This seemingly paradoxical idea is a cornerstone of quantum mechanics and is absolutely essential for understanding how the universe works at its most fundamental level. It underpins all modern technologies from lasers and transistors to medical imaging and the very concept of quantum computing.
The objects aren't just "here or there"—they are probabilistic ripples, until observed.
Wave-particle duality is nature’s way of whispering: “The world is more nuanced than it seems.”